1. 甚麼是 RL？

應用場景：

• 給機器一個輸入，但我們不知道最佳輸出為何

• 收集有標註的資料有難度

例如叫機器學習下圍棋，最好的下一步可能人類根本不知道。在不知道正確答案是什麽的情況下，就可以使用 RL

1.1 Actor

Reinforcement Learning 中有 Actor 及 Environment，Actor 跟 Environment 會進行互動。
actor 就是 RL 中要找的 function，輸入為 observation，輸出為 action，function 的目標是最大化從 environment 獲得的 reward 總和

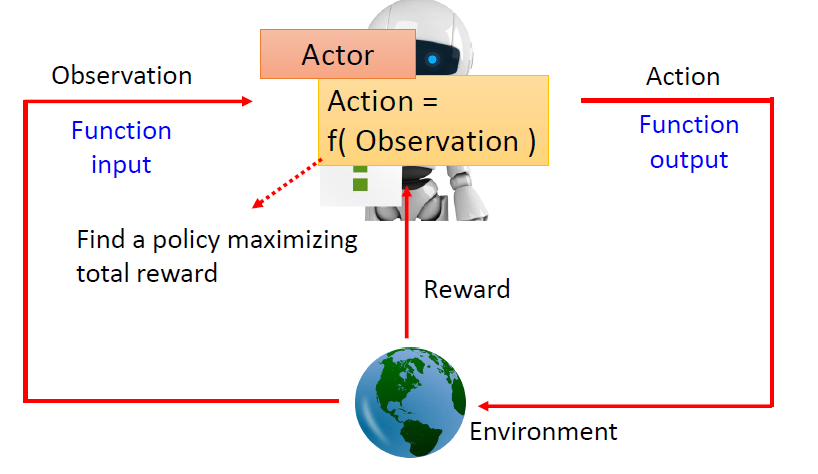
actor 以 environment 提供的 observation 作為輸入，而 actor 收到 observation 後，會輸出 action 影響 environment，environment 受到 action 的影響產生新的 observation，environment 會不斷地給 actor 一些 reward，告訴他採取的 action 好不好

Example 1：Space Invader

• actor：搖桿操控者

• environment：遊戲主機

• observation：遊戲畫面

• action：母艦向左、向右及開火

• reward：獲得的分數

要找一個 actor（function），可以使得到的 reward 的總和最大

Example 2：圍棋

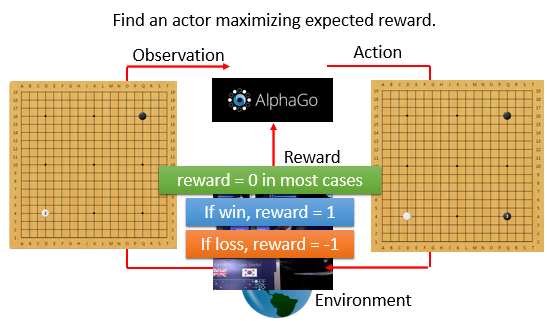
• actor ：AlphaGo

• environment：人類對手

• observation：棋盤

• action：在 $19\times19$ 的棋盤上的落子

• reward：整局結束以後，贏得 1 分，輸得 0 分。過程中不會得到 reward

要找一個 actor（function），可以使得到的 reward 的總和最大

1.2 訓練三步驟

Step 1：Function with Unknown

actor 就是一個 network，稱為 Policy Network

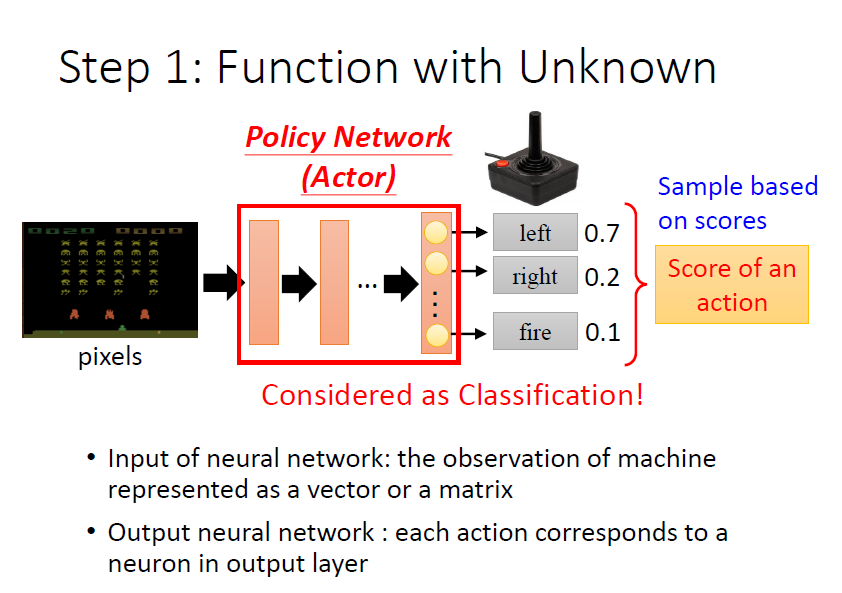
• 架構：FC、CNN、Transformer、……

• 輸入：遊戲的畫面 pixels

• 輸出：每個可採取行為的分數（向左 0.7 分、向右 0.2 分、開火 0.1 分，相加為 1）

把輸出的分數當做機率，依照這些機率 sample 出一個 action

Step 2：Define “Loss”

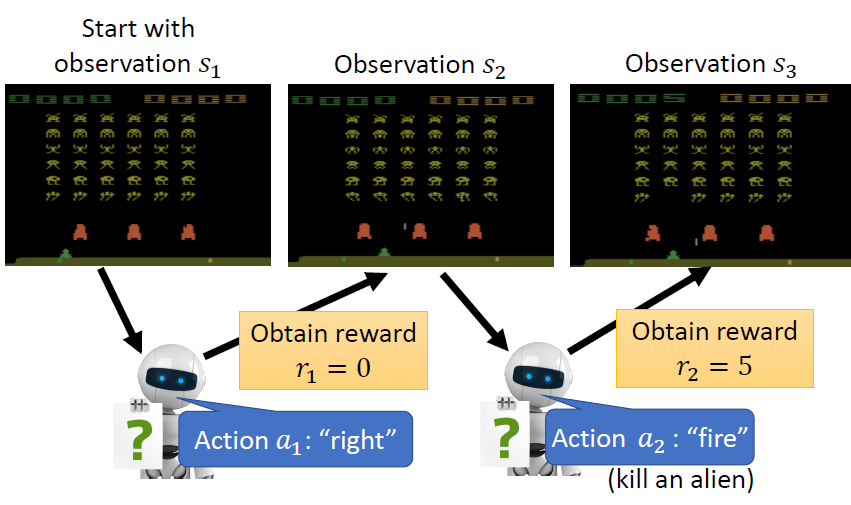
一整局遊戲稱為一個 episode，遊戲中每個行為都可能得到 reward，把所有的 reward 相加得到整場遊戲的 total reward，又稱為 return

• Reward：每個行為得到的反饋

• Return：整場遊戲得到的 reward 之和，目標是最大化 return，所以 loss 即為 $-R$

Step 3：Optimization

對環境的 observation $s_1$，會變成 actor 的輸入，actor 依此輸出 action $a_1$，$a_1$ 又作為環境的輸入，根據 $a_1$ 輸出 $s_2$，以此類推，直至滿足遊戲終止條件

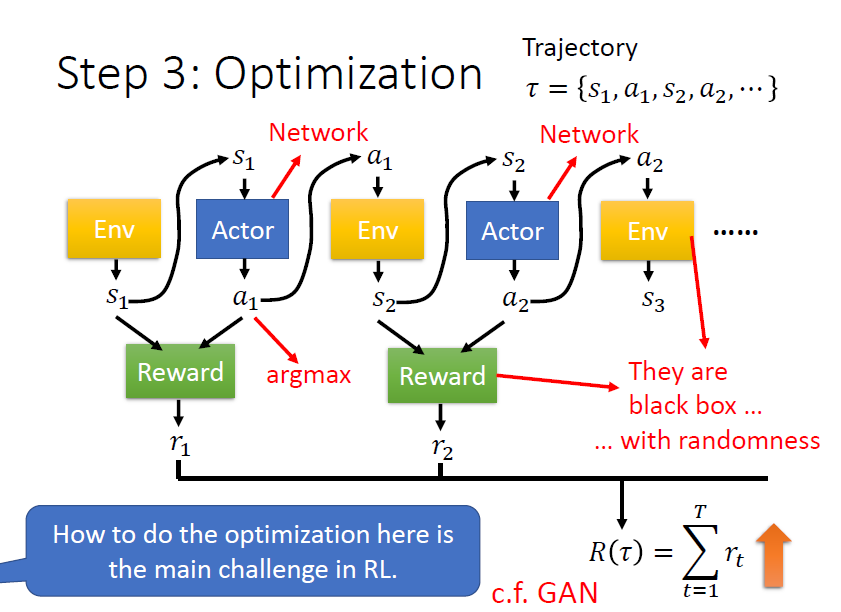
$s$ 跟 $a$ 所形成的 sequence $\{s_1,a_1,s_2,a_2,...\}$ 稱作 Trajectory，以 $\tau$ 表示

定義 reward function 會考慮 action 和 observation 兩者，把所有的 $r$ 相加得到 $R$，即是要去最大化的對象

目標：

找到 actor 的一組參數，使得 $R(\tau)$ 越大越好

問題：

1. actor 具有隨機性：由於 action 是 sample 產生的，給定相同的 $s$，產生的 $a$ 可能不一樣

2. environment 和 reward 是黑盒子：environment 和 reward 都不是 network，也都具有隨機性

總之，還是可以把 RL 看成三個階段，只是在 optimization 時，如何最小化 loss（最大化 return）跟之前學到的方法是不太一樣的

與 GAN 的異同之處

2. Optimization：Policy Gradient

更詳細介紹 Policy Gradient：https://youtu.be/W8XF3ME8G2I

2.1 如何控制 Actor

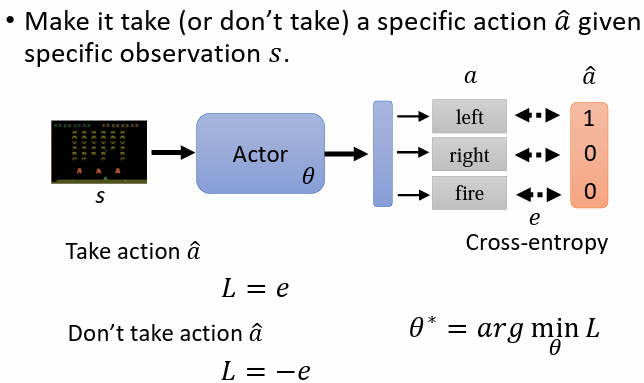
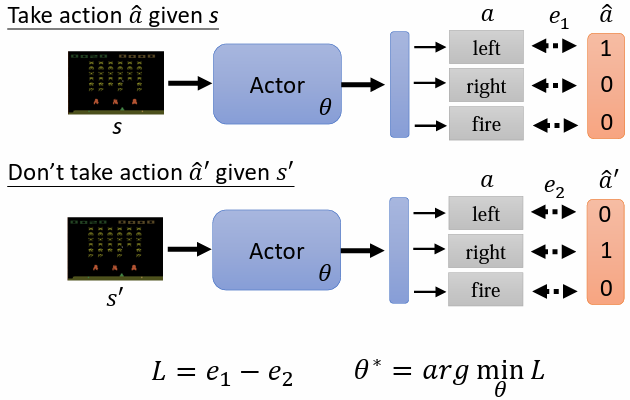
• 若希望 actor 在看到某個 $s$ 時採取某一 action，只需將其看做一般的分類問題即可，為其設定 ground truth $\hat{a}$，loss $e$ 採用 cross-entropy

• 若希望 actor 在看到某個 $s$ 時不採取某一 action，只需將 cross-entropy 乘一個負號，最小化 $L$ 等同於最大化 $e$，以使 actor 的 action 離 $\hat{a}$ 更遠

綜合以上兩種情況，可將 $L$ 定義為 $e_1-e_2$，找到一組參數最小化 $e_1$，同時最大化 $e_2$，即可最小化 loss $L$

2.2 收集訓練資料

方法：

1. 為每個行為標註為”好”或”不好”（+1、-1）

   

   收集一堆某一 observation 下應該採取或不採取某一 action 的資料
   定義 loss $L=+e_1-e_2+e_3-…-e_N$

2. 每個行為給定一個分數 $A_n$

   

   係數不再是只有正負 1
   定義 loss $L=\sum A_ne_n$

問題：

• 如何定義 $A_i$（by Version 0 ~ Version 4）

• 如何產生 $s$ 與 $a$ 的 pair

2.3 如何定義 A

Version 0 （不正確）

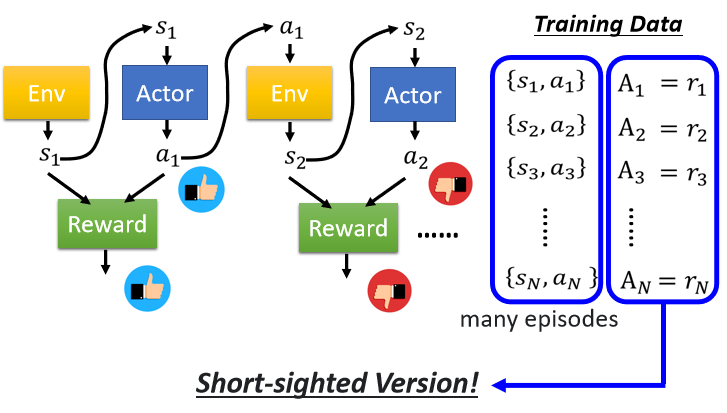
1. 首先定義一個隨機的 actor，記錄若干個 episodes 中 actor 與環境互動時，面對每一個 observation $s$ 產生的 action a

2. 對記錄下來的每個 action 計算 reward

3. 將 reward 作為 $A$ 用於定義 loss

問題：

短視近利，沒有長程規劃的概念
使用 Version 0，只要採取向左跟向右，得到的 reward 會是 0；只有開火時得到的 reward 是正的，導致機器會學到只有瘋狂開火才是對的，會一直傾向於射擊

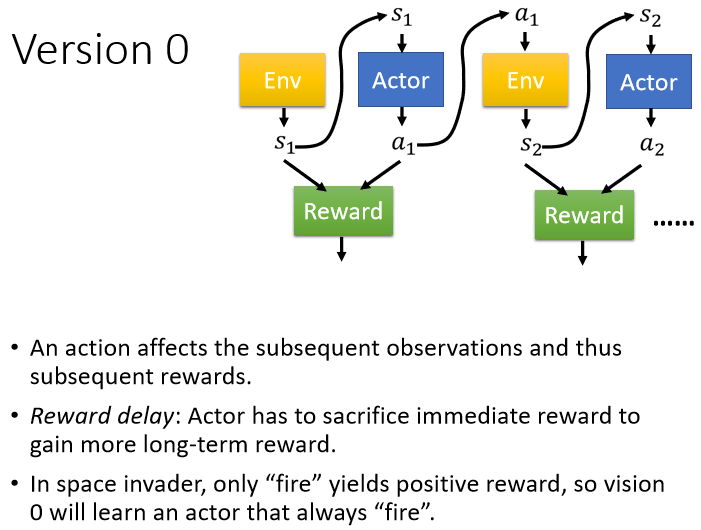
• 每一個行為並不是獨立的，每一個行為都會影響到接下來發生的事情

• Reward Delay：需要犧牲短期的利益，以換取更長程的目標

Version 1（Cumulated Reward）

Version 1 中，$a_t$ 有多好，不僅取決於 $r_t$，也取決於 $a_t$ 之後所有的 reward，也就是把 $a_t$ 當下及之後的所有 action 得到的 reward 通通加起來，得到 $G_t$（cumulated reward）

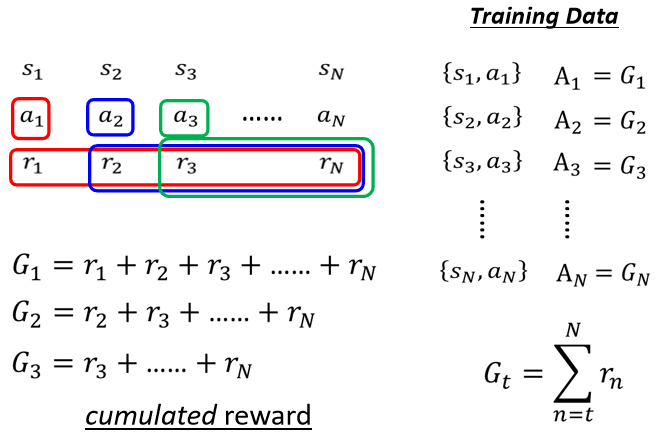
問題：

假設遊戲非常長，把 $r_N$ 歸功於 $a_1$ 也不合適

Version 2（Discounted Cumulated Reward）

改良 Version 1 的問題，新增 discount factor $\gamma$（$\gamma<1$），離 $a_t$ 比較近的 reward 給予較大的權重，較遠的 reward 給予較小的權重，使較遠的 reward 影響較小

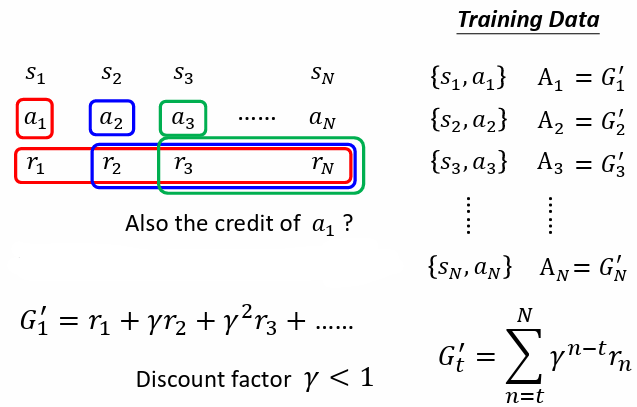
Version 3（標準化：-b）

假設某一遊戲得到的 reward 永遠都是正的，只是有大有小不同，因此每個 $G$ 都會是正的，就算某些行為是不好的，還是會鼓勵機器採取某些行為，所以需要做標準化，改良 Version 2，把所有 $G'$ 減一個 baseline $b$

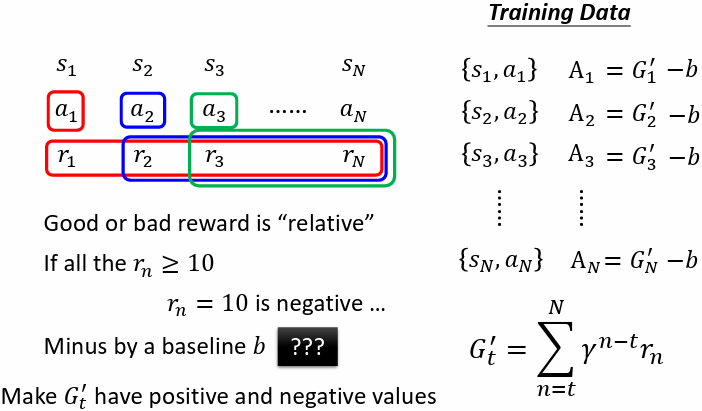
Version 3.5（b = value funtion）

訓練一個 critic，給一個 observation $s$，輸出 $V^\theta(s)$，讓 Version 3 的 $b = V^\theta(s)$

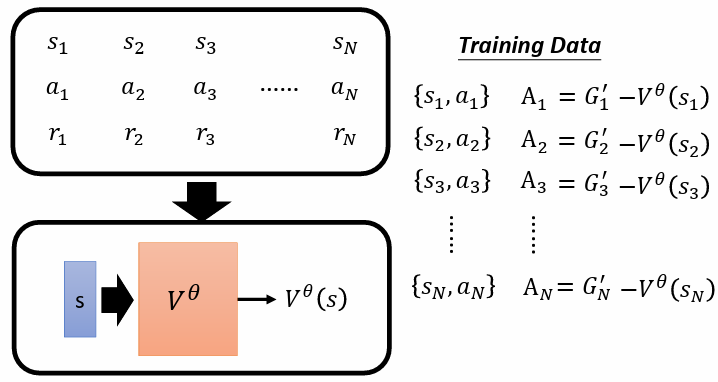
解釋：

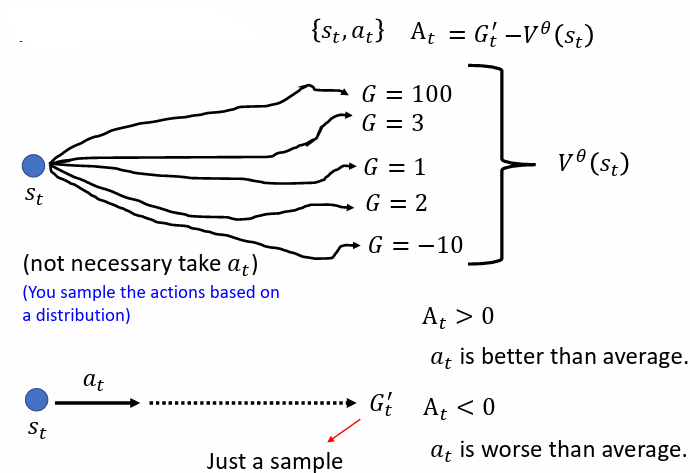
$V^\theta(s_t)$ 可以視為在 observation $s_t$ 下，actor 採取各種可能的 action 後得到的 $G'_t$ 期望值

$G'_t$ 則是真正結束一個 episode 後，得到的 discounted cumulated reward

$A_t$ 是對 actor 在 observation $s_t$ 下，採取 action $a_t$ 的評價：

• 若 $A_t>0$，表示 $G'_t>V^\theta(s_t)$，意義為採取特定 action $a_t$ 得到的 $G'_t$ 比隨機選擇一個 action 的期望值 $V^\theta(s_t)$ 好，所以給予正的評價 $A_t$

• 若 $A_t<0$，表示 $G'_t<V^\theta(s_t)$，意義為採取特定 action $a_t$ 得到的 $G'_t$ 比隨機選擇一個 action 的期望值 $V^\theta(s_t)$ 不好，所以給予負的評價 $A_t$

問題：

$A_t=G_t'-V^\theta(s_t)$ 表示用一次 sample 的結果減去所有的“平均”，似乎不夠準確

解決：

Version 4（Advantage Actor-Critic）

Version 4（Advantage Actor-Critic）

在 observation $s_t$ 下，採取 action $a_t$ 到 $s_{t+1}$，考慮在 $s_{t+1}$ 下採取各種 action $a_{t+1}$ 的情况，並求所有 $G'_{t+1}$ 的平均值（期望值）

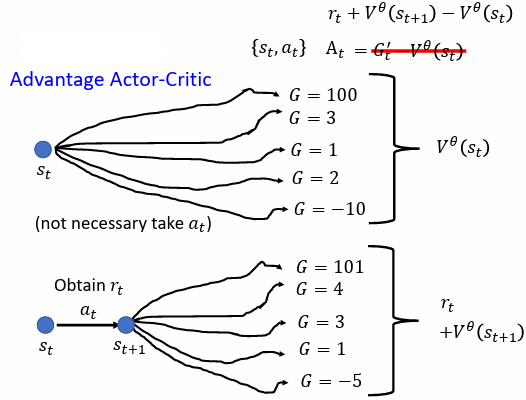
因為 value function 意義上可以代表各種 action 的平均 discounted cumulated reward，因此直接使用 $V^\theta(s_{t+1})$ 表示 $s_{t+1}$下各種 $a_{t+1}$ 得到的 $G'_{t+1}$的平均值（期望值），所以將 $G'_{t}$ 替換為 $r_t+V^\theta(s_{t+1})$

⇒ $A_t=r_t+V^\theta(s_{t+1})-V^\theta(s_{t})$

2.4 訓練過程

1. 隨機初始化 actor，參數為 $\theta^0$

2. 迭代更新 actor

   用參數為 $\theta^{i-1}$ 的 actor 蒐集資料，並以此資料計算 $A$，再計算 loss $L$，做 gradient descent 更新參數

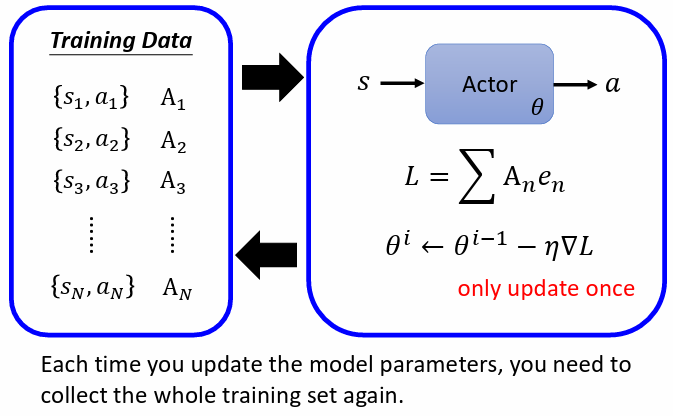
每次更新完一次參數以後，資料就要重新再收集一次，此舉非常花時間。而這麼做的目的是因為帶 $\theta^{i-1}$ 參數的 actor 收集到的資料，不一定適合拿來做為更新 $\theta^i$ 的資料

帶 $\theta^i$ 參數的 actor 與帶 $\theta^{i-1}$ 參數的 actor 採取的 action 不會一樣，因而參考過去的 trajectory 沒有意義

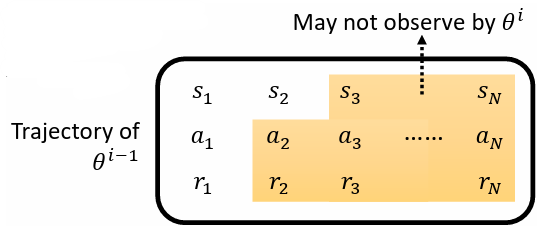
2.4.1 On-policy vs Off-policy

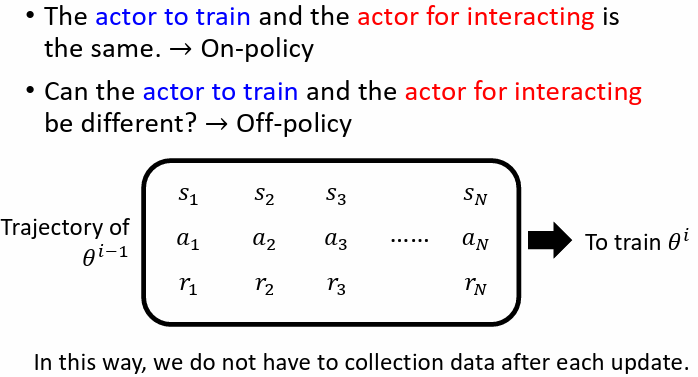
• On-policy Learning：訓練的 actor 跟與環境互動的 actor 是同一個

• Off-policy Learning：訓練的 actor 跟與環境互動的 actor 是不同的
  好處是不用一直收集資料，可以用一次收集到的資料，更新多次 actor
  Proximal Policy Optimization（PPO）即是採用 off-policy learning，細節可參考：https://youtu.be/OAKAZhFmYoI

2.4.2 Exploration（增加 actor 做 action 的隨機性）

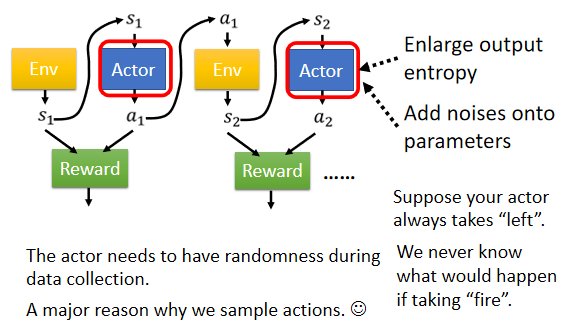
問題：

actor 所採取的 action 是 sample 而來的，因此 actor 採取的 action 具有隨機性
若一個 actor 採取行為的隨機性不夠，則一個 episode 結束後，所蒐集到的資料中有些 actions 根本沒有被 sample 到，會導致無從知道這些 actions 的好壞

解決：

期望跟環境互動的 actor 採取 actions 的隨機性要夠大，如此才能收集到比較豐富的資料
因此在訓練時，可藉由以下方式解決：

1. 刻意加大 actor 輸出的 distribution 的 entropy（比較容易 sample 到機率較低的 action）

2. 在 actor 參數上加 noise

3. …

Exploration 是 RL 訓練過程中重要的技巧

3. Critic

3.1 Value Function

有一 actor 參數為 $\theta$，當前的 observation 為 $s$，value function $V^\theta(s)$ 為基於參數為 $\theta$ 的 actor 及 observation $s$，所預期的 discounted cumulated reward（期望值的概念）

critic 做的事就是在只看到當前 $s$ 而尚未完成這局遊戲前，就得到對參數為 $\theta$ 的 actor 的評價 $V^\theta(s)$

3.2 How to train critic

兩種方法訓練 critic：Monte Carlo 及 Temporal-Difference

3.2.1 Monte Carlo（MC） Based Approach

將 actor 拿去跟環境互動很多輪（episodes），得到一些遊戲的記錄（訓練資料）

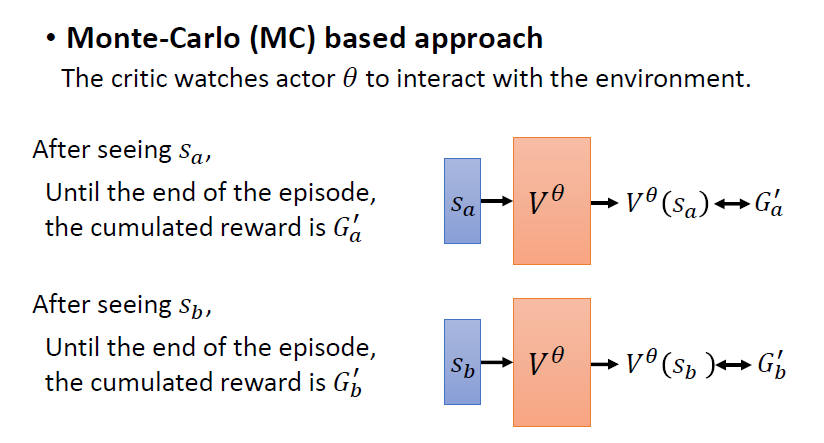
針對某一筆訓練資料，其 observation 為 $s_a$，$V^\theta(s_a)$ 要與 discounted cumulated reward $G'_a$ 越接近越好。利用這些訓練資料，訓練 critic 以輸出期待的 $V^\theta(s)$

3.2.2 Temporal-Difference（TD） Approach

不需玩完整場遊戲（一個 episode）得到訓練資料。只要在看到 observation $s_t$， actor 執行 action $a_t$，得到 reward $r_t$，接下來再看到 observation $s_{t+1}$，就能夠更新一次 critic 參數。此方法對於很長的遊戲或玩不完的遊戲非常合適

觀察：

$V^\theta(s_t)$ 和 $V^\theta(s_{t+1})$ 之間有著代數關係：$V^\theta(s_t) = \gamma V^\theta(s_{t+1})+r_t$
移項後可得：$V^\theta(s_t)-\gamma V^\theta(s_{t+1})=r_t$

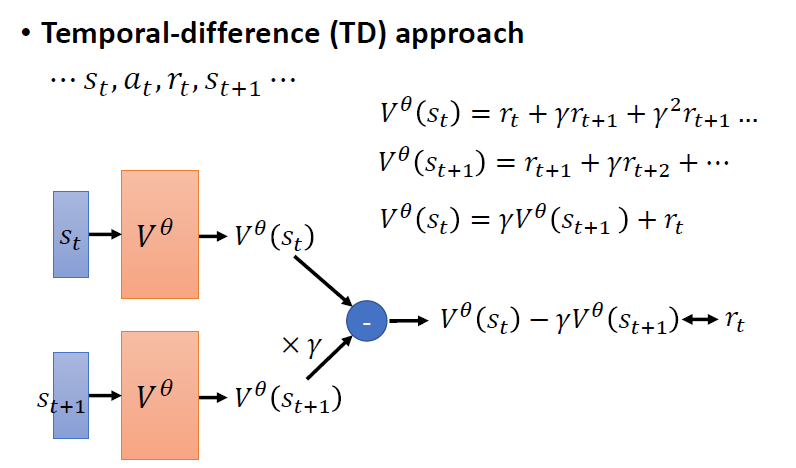
擁有 $s_t,a_t,r_t,s_{t+1}$ 訓練資料，即可計算 $V^\theta(s_t)-\gamma V^\theta(s_{t+1})$，目標希望與 $r_t$ 越接近越好

3.2.3 MC vs TD

由於 MC 與 TD 的背後的假設不同，訓練得到的 critic 也不同

MC 與 TD 得到的 $V^\theta(s_b)$ 都為 3/4，但 MC 得到的 $V^\theta(s_a)$ 為 0，而 TD 得到的 $V^\theta(s_a)$ 為 3/4

使用 critic 於訓練 actor 上：Version 3.5、Version 4

4. Tip of Actor-Critic

actor 與 critic 都是一個 network，兩者皆以 observation $s$ 作為輸入，actor 輸出每一個 action 的機率分布；critic 輸出一個數值 $V^\theta(s)$

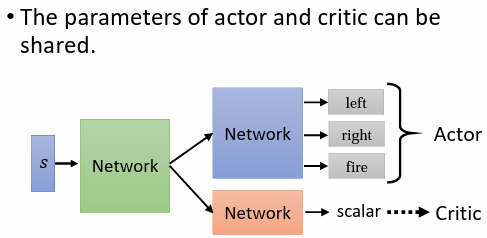
可將 actor 及 critic 兩個 network，共用部分的 network

5. To Learn More：DQN

直接使用 critic 決定要採取什麼 action，最知名的做法就是 Deep Q Network（DQN），細節可參考：https://youtu.be/o_g9JUMw1Oc、https://youtu.be/2zGCx4iv_k

DQN 的變形：Rainbow: Combining Improvements in Deep Reinforcement Learning（Rainbow）

6. Reward Shaping

6.1 Sparse Reward

問題：

Sparse Reward 就是 reward 大多數情況都是 0，只有在少數情況是一個非常大的數值。意味著很多 actions 無從判斷是好是壞。例如圍棋到遊戲結束才會有 reward，過程中都沒有 reward

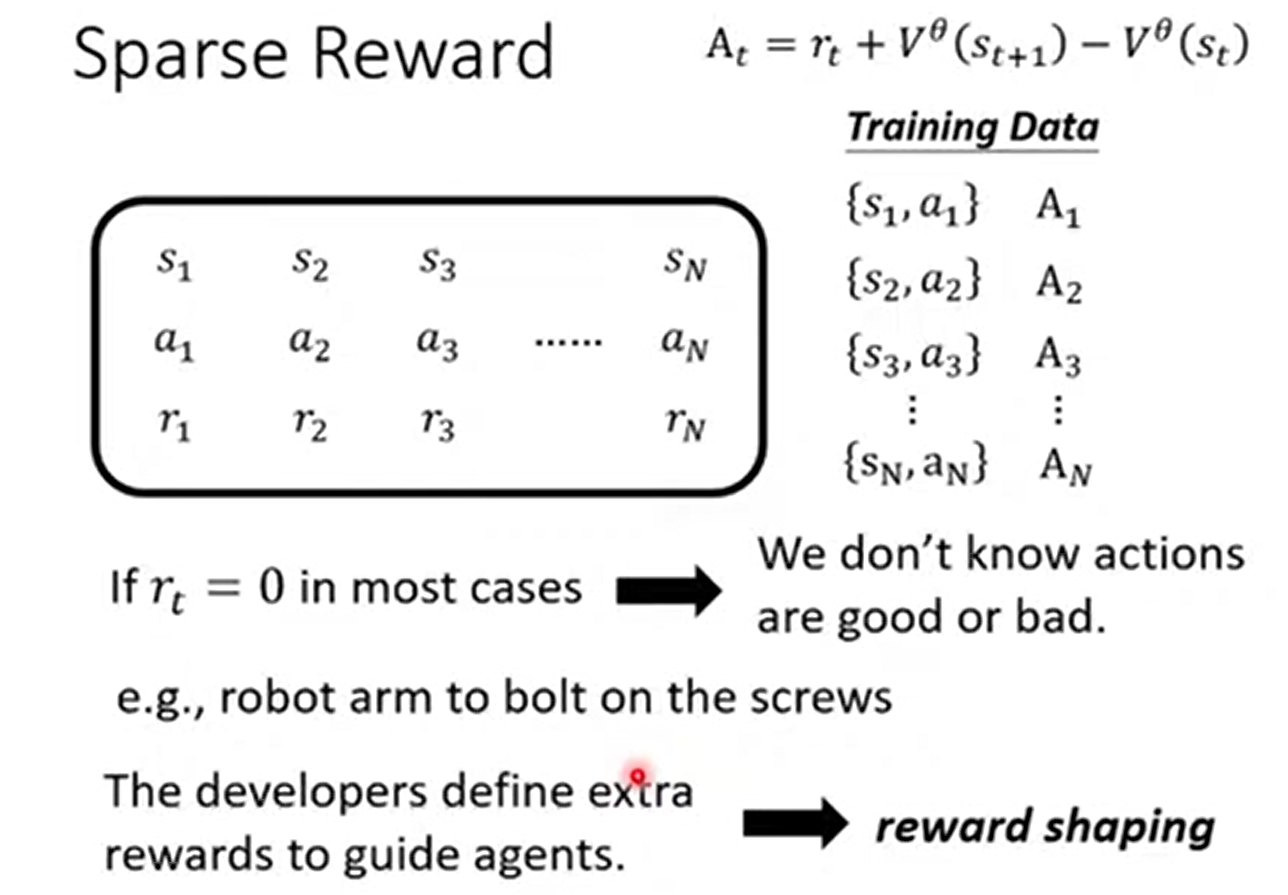
解決：

Reward Shaping：定義一些額外的 reward 來幫助 actor 學習

舉例：

如射擊類遊戲，除贏得勝利得到 +reward 及輸掉遊戲得到 - reward 外，額外定義了其他行為可以得到正的或負的 reward，如撿到補血包（＋）、待在原地（+）、存活（-）等等

因此 reward shaping 都要倚靠人類的 domain knowledge 來定義

6.2 Curiosity

reward shaping 的其中一種做法：Curiosity based reward shaping

基於好奇心，讓 actor 看到有意義的新東西時獲得 reward

7. No Reward：Imitation Learning

問題：

• 遊戲中雖然容易定義 reward，但在其他任務要定義 reward 很困難

• 人工設置一些 reward（reward shaping）教機器學時，若 reward 沒設定好，機器可能會產生奇怪、無法預期的行為

解決：

沒有 reward 的狀況下，可使用 imitation learning

7.1 Imitation Learning

在沒有 reward 的情況下訓練 actor

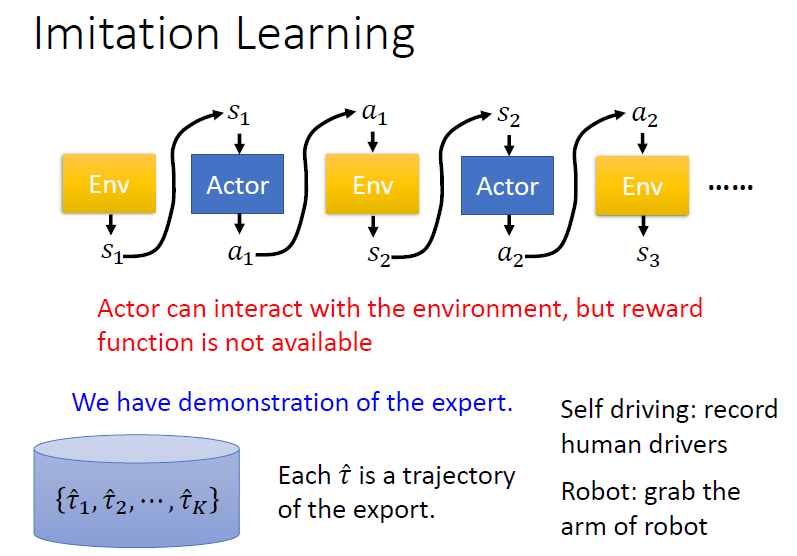
引入 expert（通常為人類）的示範。找很多 experts 跟環境互動，記錄互動的結果 $\hat{\tau}$，每個 $\hat{\tau}$ 代表一個 trajectory

舉例：

• 自動駕駛：記錄人類的駕駛行為

• 機械手臂：拉著機器的手臂示範

7.1.1 Behavior Cloning

類似於監督式學習，讓機器做出的 action 跟 export 做出的 action 越接近越好，又稱作 Behavior Cloning

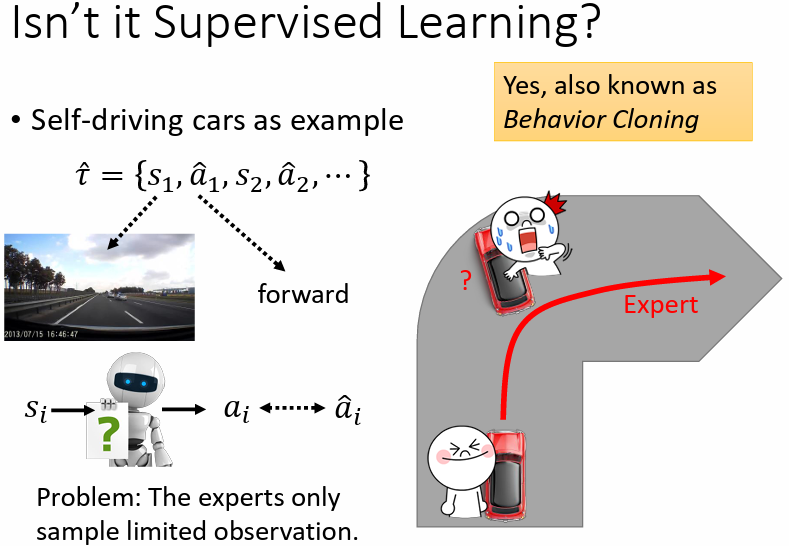
問題：

• experts 的記錄有限，若 actor 遇到從沒見過的情境，可能會做出無法預期的 action

• experts 做出的一些 actions actor 並不一定需要學習模仿，模仿的行為可能不會帶來好的結果

7.1.2 Inverse Reinforcement Learning

從 expert 的 demonstration，還有 environment 去反推 reward funtion，學出一個 reward funtion 後，再用一般的 RL 來訓練 actor

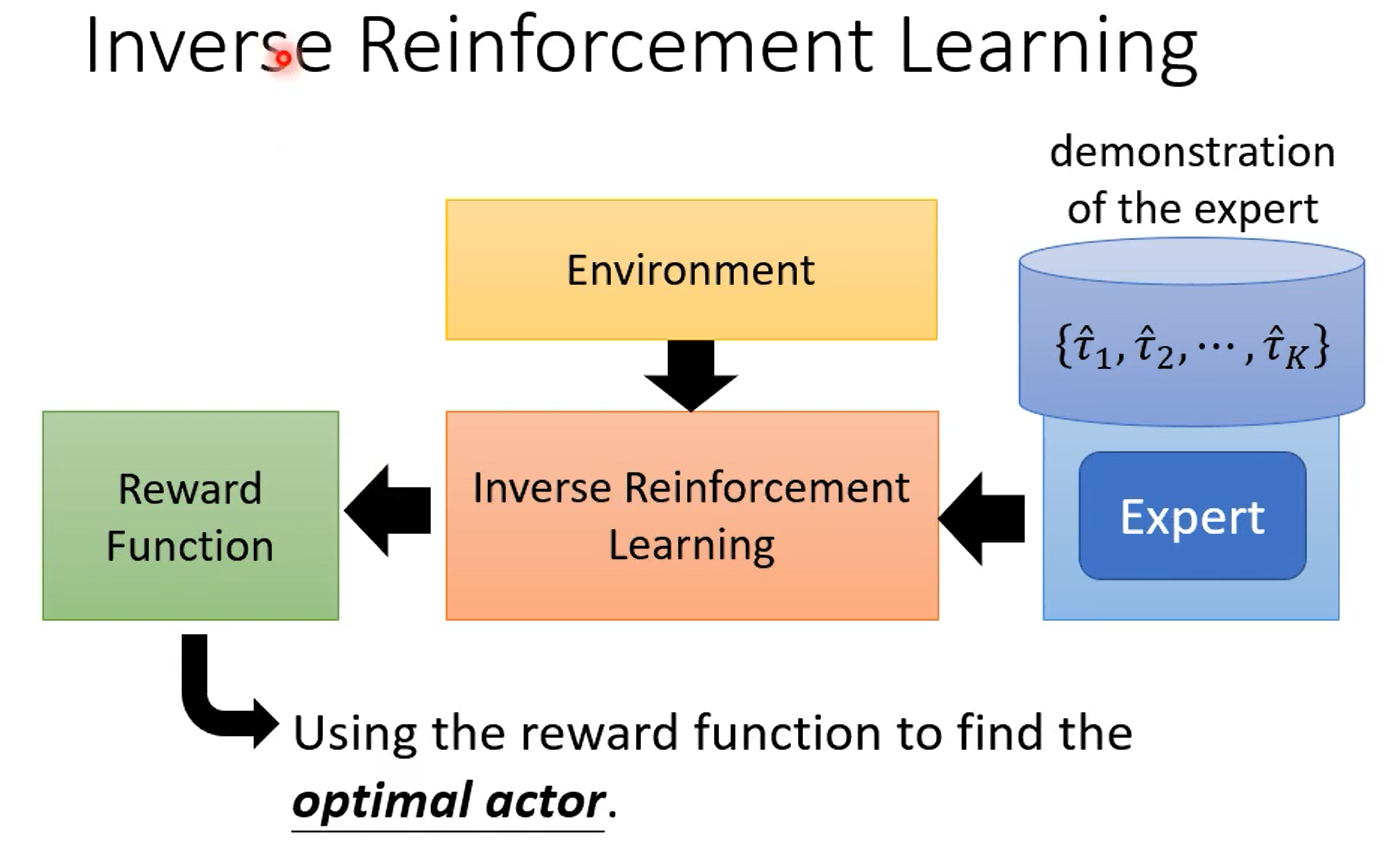
如何找出 reward funtion？

原則：teacher 的行為總是最好的

步驟：

1. 初始化一個 actor

2. 迭代訓練
   1. actor 與環境互動獲得多個 trajectory $\tau$
   2. 定義（更新）一個 reward function，能夠使老師的 reward 總和 $\Sigma R(\hat{\tau})$ 比 actor 的 reward 總和 $\Sigma R({\tau})$ 更高
   3. 利用定義的 reward function 進行訓練，更新 actor 的參數，使 actor 能夠最大化 reward

3. 輸出 reward function 以及訓練得到的 actor

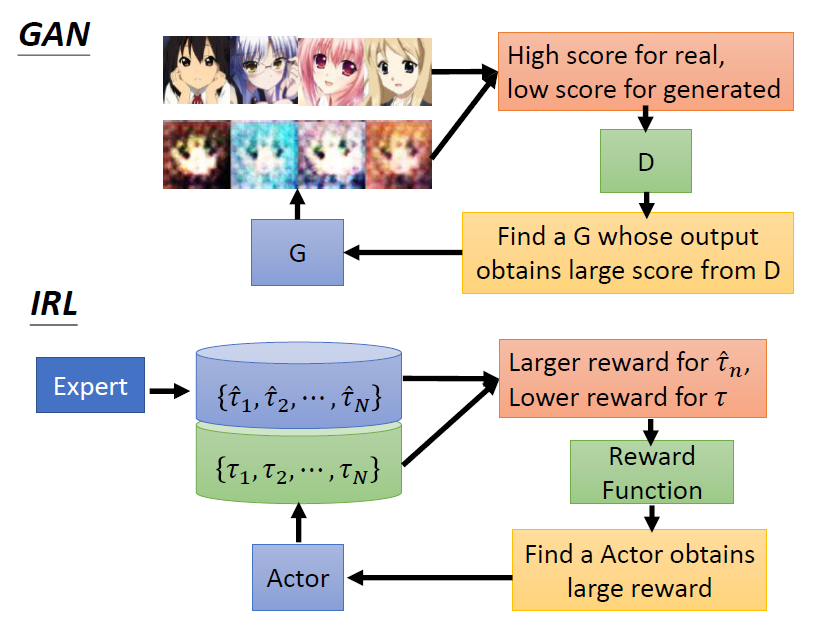
GAN vs IRL

IRL 就如同 GAN，actor 可視為 generator；reward function 可視為 discriminator